About Me
I am an ai scientist and Assistant Professor of Biomedical Informatics at the Mayo Clinic, where I lead the ai and Data Analytics (aida) team in the Department of Radiation Oncology. We develop next-generation ai systems to advance cancer diagnosis and treatment. See my faculty page for research areas.
Before joining Mayo, I was a senior researcher at Microsoft Research in Cambridge, uk, where I developed generative deep learning models for proteins in the ai for Science team. Our work on BioEmu was featured on the front cover of Science.
I earned my ph.d. in machine learning from the University of Cambridge, advised by Professor Richard E. Turner. My research, combining probabilistic modeling and deep learning, was published at leading machine learning conferences including neurips, iclr, and icml.
See my selected papers, or visit my Google Scholar profile for a full list.
contact: foong.andrew@mayo.edu
Experience

ai scientist, senior associate consultant
assistant professor of biomedical informatics
mayo clinic
January 2025 – present
Rochester, Minnesota, usa
Department of Radiation Oncology
ai for cancer treatment

senior researcher
microsoft research
November 2022 – November 2024
Cambridge, uk
ai for Science team
Generative deep learning for protein structure

ph.d. in machine learning
university of cambridge
October 2018 – November 2022
Cambridge, uk
Computational and Biological Learning Laboratory
Supervisor: Professor Richard E. Turner
Deep learning · Probabilistic modeling

research scientist intern
google deepmind
February 2022 – May 2022
London, uk
Supervisor: Dr. Michalis Titsias
Deep generative modeling · Gaussian processes

research intern
microsoft research
July 2021 – October 2021
Cambridge, uk
Supervisor: Dr. Sebastian Nowozin
Deep learning for molecular dynamics simulation

b.a. & m.eng. in information and computer engineering
university of cambridge
October 2014 – July 2018
Cambridge, uk
Department of Engineering
First class honours with distinction, top 1–2% in year group
Research Papers
For a full list of research papers, see my Google Scholar page. Daggers† denote co-first authorship.
2025
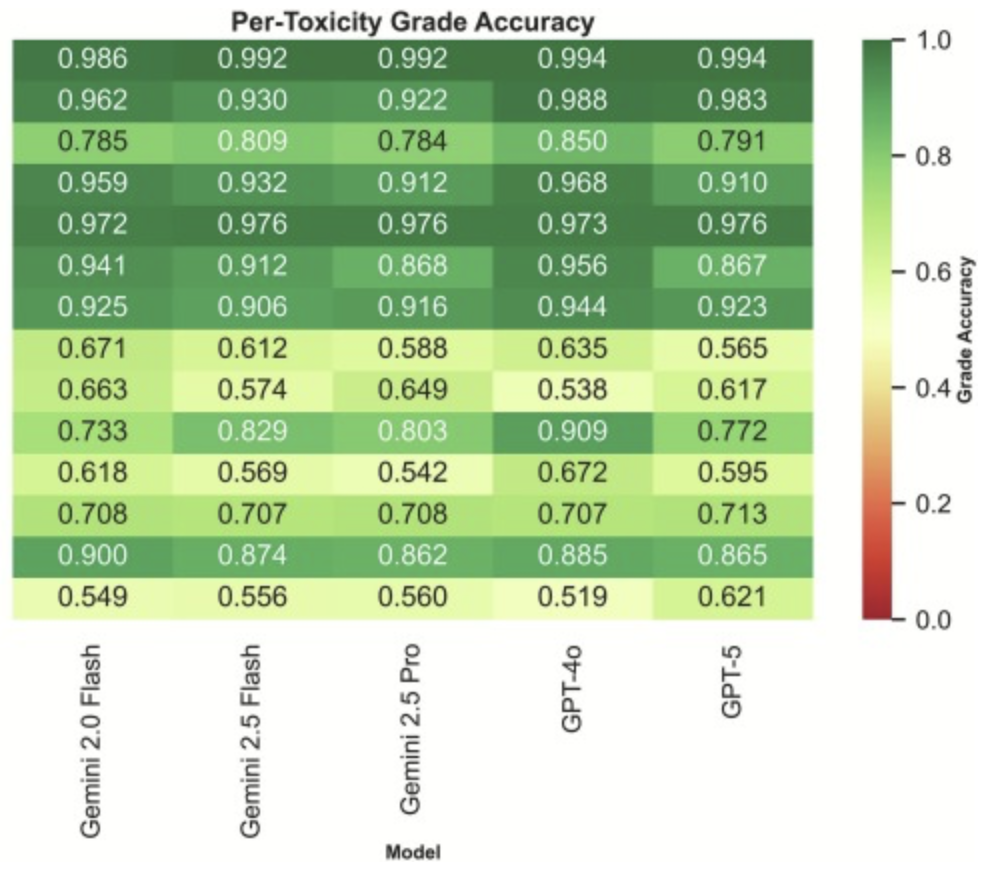
Large Language Models for Toxicity Extraction in Oncology Trials: A Real-World Benchmark in Prostate Radiotherapy
Radiotherapy and Oncology
Federico Mastroleo, Mariana Borras-Osorio, Shiv Patel, Sarah Peterson, Renthony Wilson, Mi Zhou, Satomi Shiraishi, Andrew Y. K. Foong, David Routman, Mark R. Waddle
This study evaluates the accuracy and cost-effectiveness of off-the-shelf large language models for extracting ctcae-graded toxicities from a prospective prostate radiotherapy trial. The results show that modern llms achieve near-human inter-rater reliability at low cost, supporting their feasibility for scalable toxicity monitoring in clinical research despite remaining limitations in grade-level accuracy.
abstract
Background: Accurate toxicity assessment is critical in oncology trials, yet current reporting frameworks such as the Common Terminology Criteria for Adverse Events (ctcae) remain labor-intensive and subject to inter-observer variability. Large language models (llms) offer potential to automate extraction and grading of adverse events from clinical notes and patient-reported outcomes (pros), but their comparative performance and cost-effectiveness remain underexplored. Methods: We evaluated five off-the-shelf llms (Gemini 2.0 Flash, Gemini 2.5 Flash, Gemini 2.5 Pro, gpt-4o, and gpt-5) using a rule-augmented few-shot prompting strategy to extract ctcae-graded gastrointestinal and genitourinary toxicities from a prospective prostate radiotherapy trial (nct02874014; n = 55 patients, 8,968 toxicity records). Binary and grade-level accuracy, precision, recall, specificity, f1 score, Cohen’s kappa, and computational costs were assessed. Results: All models achieved high binary accuracy (84.6–87.4 %) and moderate grade accuracy (79.1–82.3 %). gpt-4o reached the best binary (87.4 %) and grade (83.5 %) accuracy, while Gemini 2.5 Pro demonstrated highest sensitivity (74.0 %). Specificity peaked with gpt-4o (96.0 %). Cohen’s kappa values indicated moderate agreement (0.552–0.560 for binary; 0.401–0.465 for grades). Costs for the entire extraction varied substantially: Gemini 2.0 Flash delivered competitive accuracy at $0.77 total, whereas Gemini 2.5 Pro and gpt-5 exceeded $21. Conclusions: Off-the-shelf llms can extract clinically relevant toxicities with performance approaching human inter-rater reliability, at variable but often negligible costs. While grade-level accuracy remains limited, llm integration into oncology workflows is feasible, offering scalable, low-cost support for toxicity monitoring and data abstraction in clinical research.
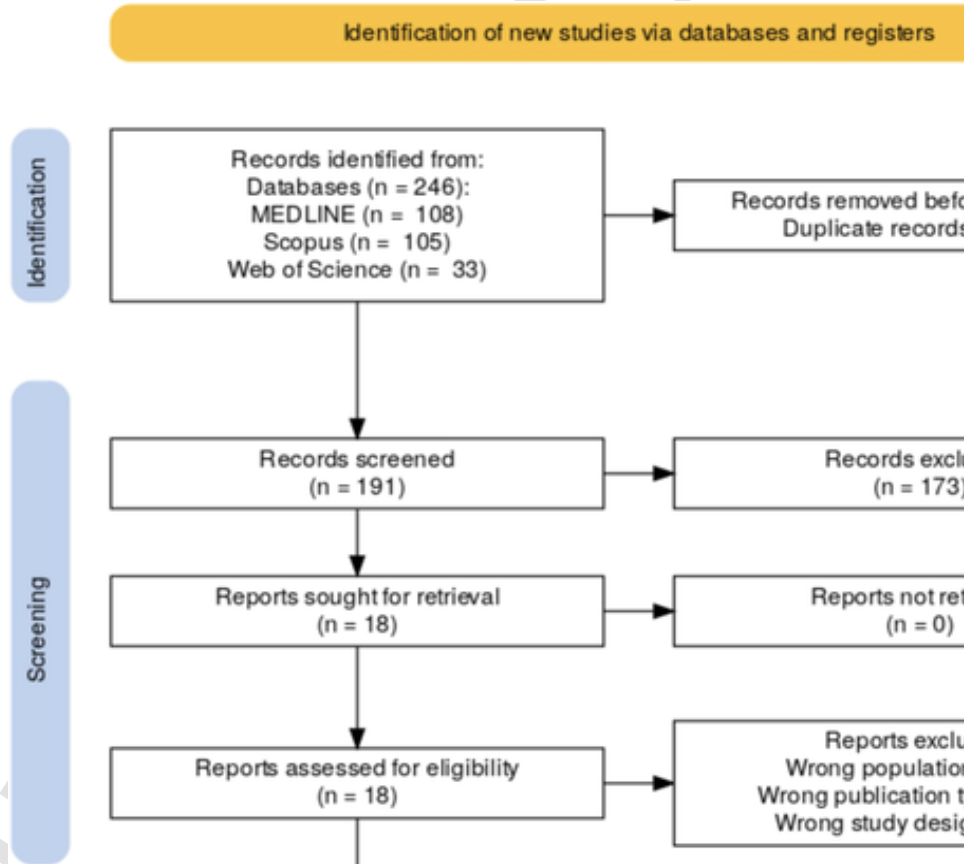
From BERT to GPT-4: A Systematic Review of AI-Driven Toxicity Extraction and Grading in Radiation Oncology
Technical Innovations & Patient Support in Radiation Oncology
Federico Mastroleo, Mariana Borras-Osorio, Shiv Patel, Sarah Peterson, Renthony Wilson, Mohammad Javad Namazi, Mi Zhou, Satomi Shiraishi, Andrew Y. K. Foong, David Routman, Mark R. Waddle
This systematic review examines how natural language processing and large language models are being used to extract and synthesize toxicity data from radiation oncology records. Across five studies, current approaches demonstrate promise but remain limited by single-center data, generalizability challenges, and computational and privacy constraints, highlighting the need for scalable, secure multi-center solutions.
abstract
Background: Toxicity assessment is a fundamental component of radiation therapy patient management. Natural language processing (nlp) and large language models (llms) are transforming clinical practice by efficiently extracting and synthesizing information from electronic health records (ehrs). This systematic review evaluates the current literature on the use of nlp and llms to extract toxicity data from radiation oncology records. Methods: Three databases were systematically searched on 14 March 2025 for English-language studies. Two reviewers screened the articles and extracted available data. Discrepancies were resolved by a third reviewer. The review adhered to prisma guidelines. Results: We identified 246 manuscripts; after screening, five studies were included. Four studies focused on identifying toxicity terms and linking them to ctcae terms, while severity grading or longitudinal tracking of toxicities was addressed by two studies. One study explored the summarization capabilities of llm to convert free text or patient surveys into concise clinician notes/chatbot responses. Included studies utilized transformer models (bert, Biobert, Clinical Longformer) for recognition and grading tasks; rule-based systems (Apache ctakes, ideal-x) used dictionaries and negation detection rules for toxicity identification. gpt-4 demonstrated zero-shot summarization and response capabilities for patient-reported outcomes. All included studies were single-center. Common challenges identified were limited generalizability, difficulty recognizing rare or negated toxicities, privacy concerns, and substantial computing requirements for fine-tuning transformer-based models. Conclusions: Current research primarily focused on three basic tasks and three categories of models. Multi-center datasets and secure, lightweight deployment methods are needed before widespread integration into routine radiation oncology practice can be considered.
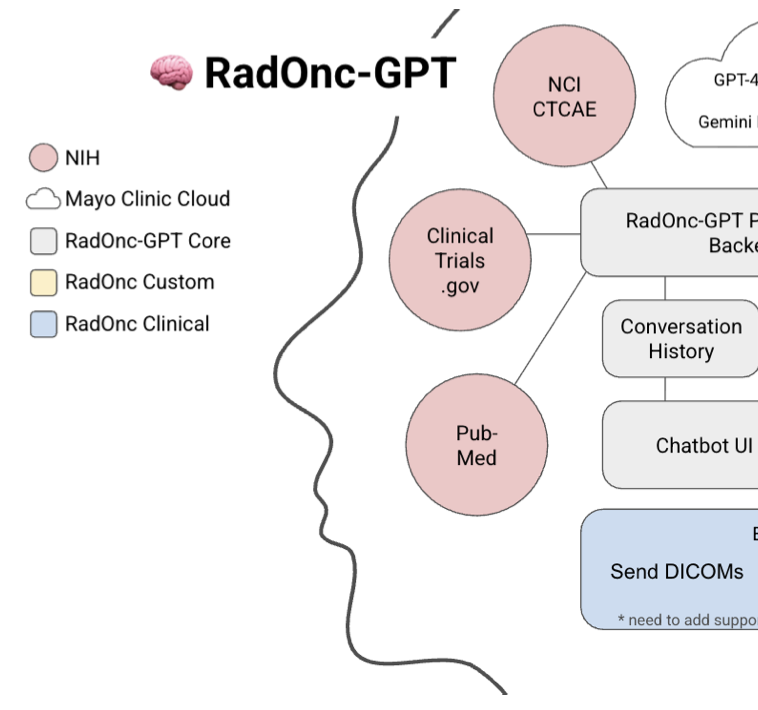
RadOnc-GPT: An Autonomous LLM Agent for Real-Time Patient Outcomes Labeling at Scale
arXiv preprint
Jason Holmes, Yuexing Hao, Mariana Borras-Osorio, Federico Mastroleo, Santiago Romero Brufau, Valentina Carducci, Katie M. Van Abel, David M. Routman, Andrew Y. K. Foong, Liv M. Muller, Satomi Shiraishi, Daniel K. Ebner, Daniel J. Ma, Sameer R. Keole, Samir H. Patel, Mirek Fatyga, Martin Bues, Brad J. Stish, Yolanda I. Garces, Michelle A. Neben Wittich, Robert L. Foote, Sujay A. Vora, Nadia N. Laack, Mark R. Waddle, Wei Liu
RadOnc-gpt is an autonomous large language model agent designed to replace manual labeling by retrieving patient-specific data, synthesizing structured and unstructured clinical evidence, and producing real-time, structured outcomes at scale in radiation oncology. We validate the system across a tiered framework, demonstrating reliable structured data retrieval and accurate labeling of complex clinical outcomes, including osteoradionecrosis and cancer recurrence across independent cohorts.
abstract
Manual labeling limits the scale, accuracy, and timeliness of patient outcomes research in radiation oncology. We present RadOnc-gpt, an autonomous large language model (llm)-based agent capable of independently retrieving patient-specific information, iteratively assessing evidence, and returning structured outcomes. Our evaluation explicitly validates RadOnc-gpt across two clearly defined tiers of increasing complexity: (1) a structured quality assurance (qa) tier, assessing the accurate retrieval of demographic and radiotherapy treatment plan details, followed by (2) a complex clinical outcomes labeling tier involving determination of mandibular osteoradionecrosis (orn) in head-and-neck cancer patients and detection of cancer recurrence in independent prostate and head-and-neck cancer cohorts requiring combined interpretation of structured and unstructured patient data. The qa tier establishes foundational trust in structured-data retrieval, a critical prerequisite for successful complex clinical outcome labeling.
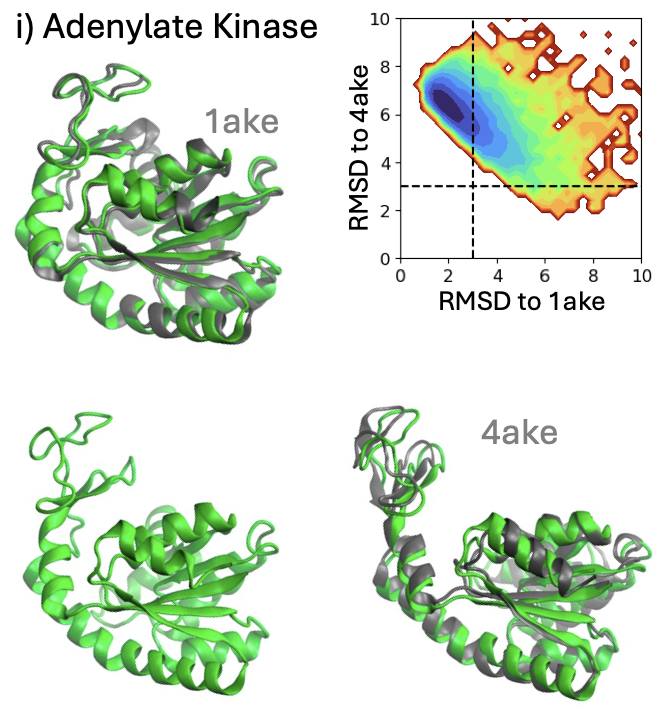
Scalable Emulation of Protein Equilibrium Ensembles With Generative Deep Learning
Science
Sarah Lewis†, Tim Hempel†, José Jiménez-Luna†, Michael Gastegger†, Yu Xie†, Andrew Y. K. Foong†, Victor García Satorras†, Osama Abdin†, Bastiaan S. Veeling†, Iryna Zaporozhets, Yaoyi Chen, Soojung Yang, Arne Schneuing, Jigyasa Nigam, Federico Barbero, Vincent Stimper, Andrew Campbell, Jason Yim, Marten Lienen, Yu Shi, Shuxin Zheng, Hannes Schulz, Usman Munir, Cecilia Clementi, Frank Noé
BioEmu is a generative deep-learning model that rapidly predicts the diverse shapes proteins adopt in nature, dramatically speeding up analyses that typically require lengthy molecular simulations. By efficiently uncovering functionally important protein movements, BioEmu accelerates drug discovery and provides a powerful computational tool to explore biological mechanisms previously inaccessible due to technical limitations.
abstract
Following the sequence and structure revolutions, predicting the dynamical mechanisms of proteins that implement biological function remains an outstanding scientific challenge. Several experimental techniques and molecular dynamics (md) simulations can, in principle, determine conformational states, binding configurations and their probabilities, but suffer from low throughput. Here we develop a Biomolecular Emulator (BioEmu), a generative deep learning system that can generate thousands of statistically independent samples from the protein structure ensemble per hour on a single graphical processing unit. By leveraging novel training methods and vast data of protein structures, over 200 milliseconds of md simulation, and experimental protein stabilities, BioEmu’s protein ensembles represent equilibrium in a range of challenging and practically relevant metrics. Qualitatively, BioEmu samples many functionally relevant conformational changes, ranging from formation of cryptic pockets, over unfolding of specific protein regions, to large-scale domain rearrangements. Quantitatively, BioEmu samples protein conformations with relative free energy errors around 1 kcal/mol, as validated against millisecond-timescale md simulation and experimentally-measured protein stabilities. By simultaneously emulating structural ensembles and thermodynamic properties, BioEmu reveals mechanistic insights, such as the causes for fold destabilization of mutants, and can efficiently provide experimentally-testable hypotheses.
2023
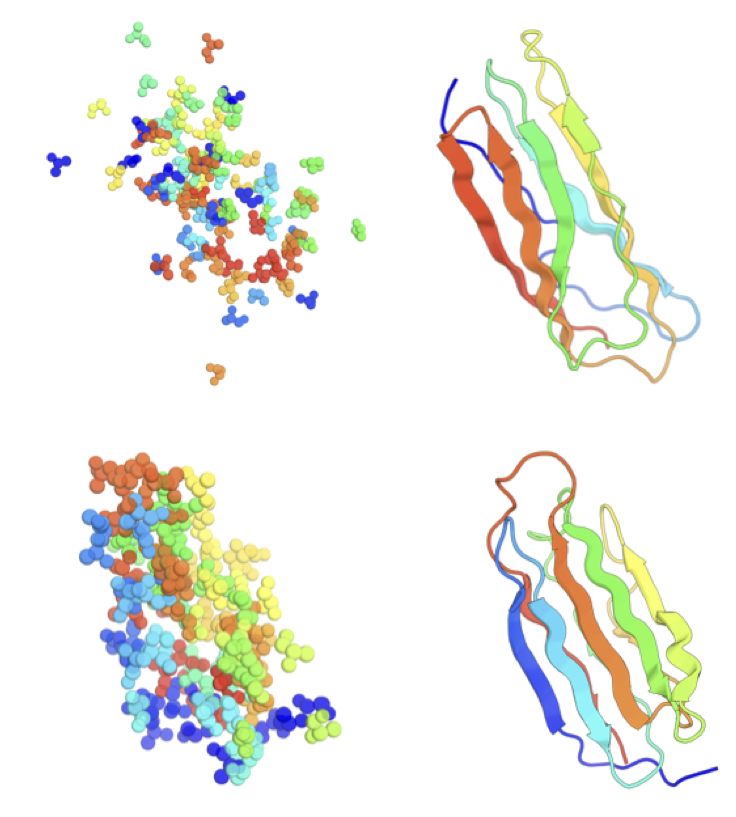
Fast Protein Backbone Generation with SE(3) Flow Matching
neurips Machine Learning for Structural Biology workshop (mlsb)
Jason Yim, Andrew Campbell, Andrew Y. K. Foong, Michael Gastegger, José Jiménez-Luna, Sarah Lewis, Victor Garcia Satorras, Bastiaan S. Veeling, Regina Barzilay, Tommi Jaakkola, Frank Noé
FrameFlow is a generative model that rapidly produces realistic protein backbones by using flow matching on the se(3) geometry group, significantly improving computational efficiency over previous diffusion-based approaches. By generating higher-quality proteins at a fraction of the computational cost, FrameFlow streamlines the design of novel proteins, making drug development and biological research more efficient.
abstract
We present FrameFlow, a method for fast protein backbone generation using se(3) flow matching. Specifically, we adapt FrameDiff, a state-of-the-art diffusion model, to the flow-matching generative modeling paradigm. We show how flow matching can be applied on se(3) and propose modifications during training to effectively learn the vector field. Compared to FrameDiff, FrameFlow requires five times fewer sampling timesteps while achieving two fold better designability. The ability to generate high quality protein samples at a fraction of the cost of previous methods paves the way towards more efficient generative models in de novo protein design.
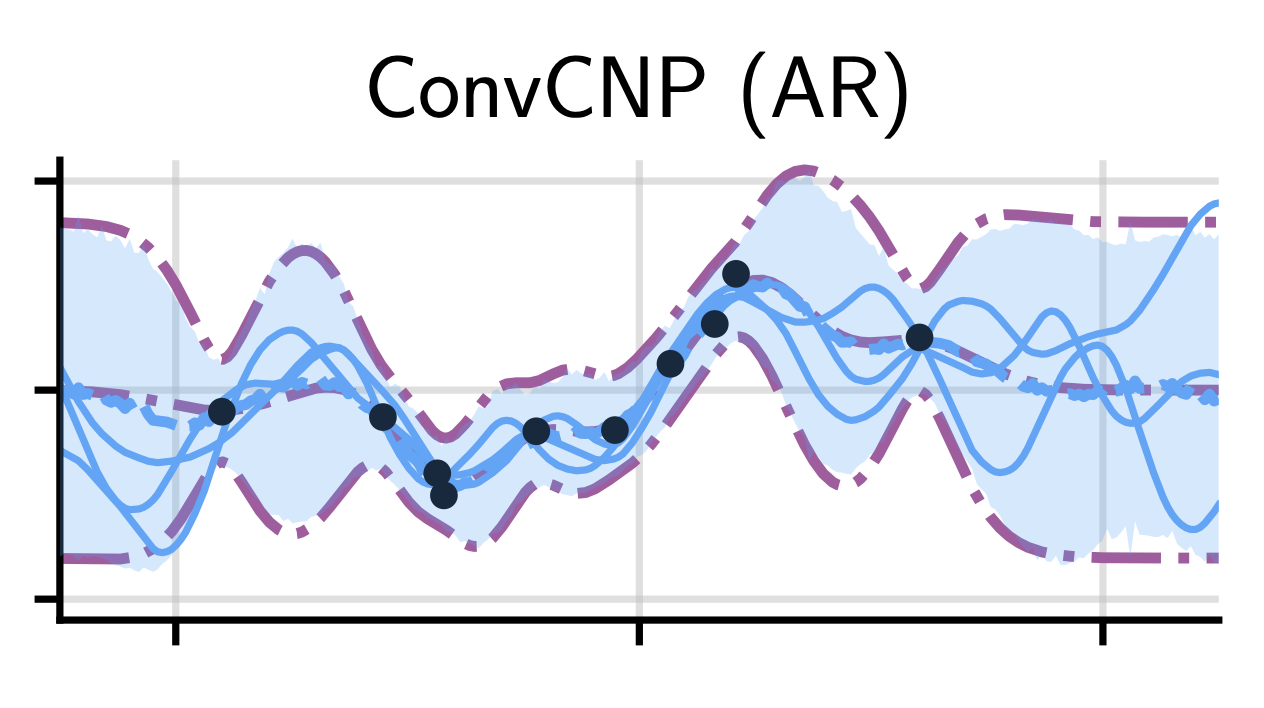
Autoregressive Conditional Neural Processes
International Conference on Learning Representations (iclr)
Wessel Bruinsma†, Stratis Markou†, James Requeima†, Andrew Y. K. Foong†, Anna Vaughan, Tom Andersson, Anthony Buonomo, Scott Hosking, Richard E. Turner
Autoregressive Conditional Neural Processes enhance the flexibility of Conditional Neural Processes (popular meta-learning models) by making predictions sequentially rather than independently, without complicating training or requiring approximate inference. This simple yet powerful approach enables accurate modeling of complex dependencies in data, achieving results competitive with sophisticated models at substantially reduced computational cost, which is particularly valuable in tasks like clinical time-series prediction.
abstract
Conditional neural processes (cnps; Garnelo et al., 2018a) are attractive meta-learning models which produce well-calibrated predictions and are trainable via a simple maximum likelihood procedure. Although cnps have many advantages, they are unable to model dependencies in their predictions. Various works propose solutions to this, but these come at the cost of either requiring approximate inference or being limited to Gaussian predictions. In this work, we instead propose to change how cnps are deployed at test time, without any modifications to the model or training procedure. Instead of making predictions independently for every target point, we autoregressively define a joint predictive distribution using the chain rule of probability, taking inspiration from the neural autoregressive density estimator (nade) literature. We show that this simple procedure allows factorised Gaussian cnps to model highly dependent, non-Gaussian predictive distributions. Perhaps surprisingly, in an extensive range of tasks with synthetic and real data, we show that cnps in autoregressive (ar) mode not only significantly outperform non-ar cnps, but are also competitive with more sophisticated models that are significantly more computationally expensive and challenging to train.
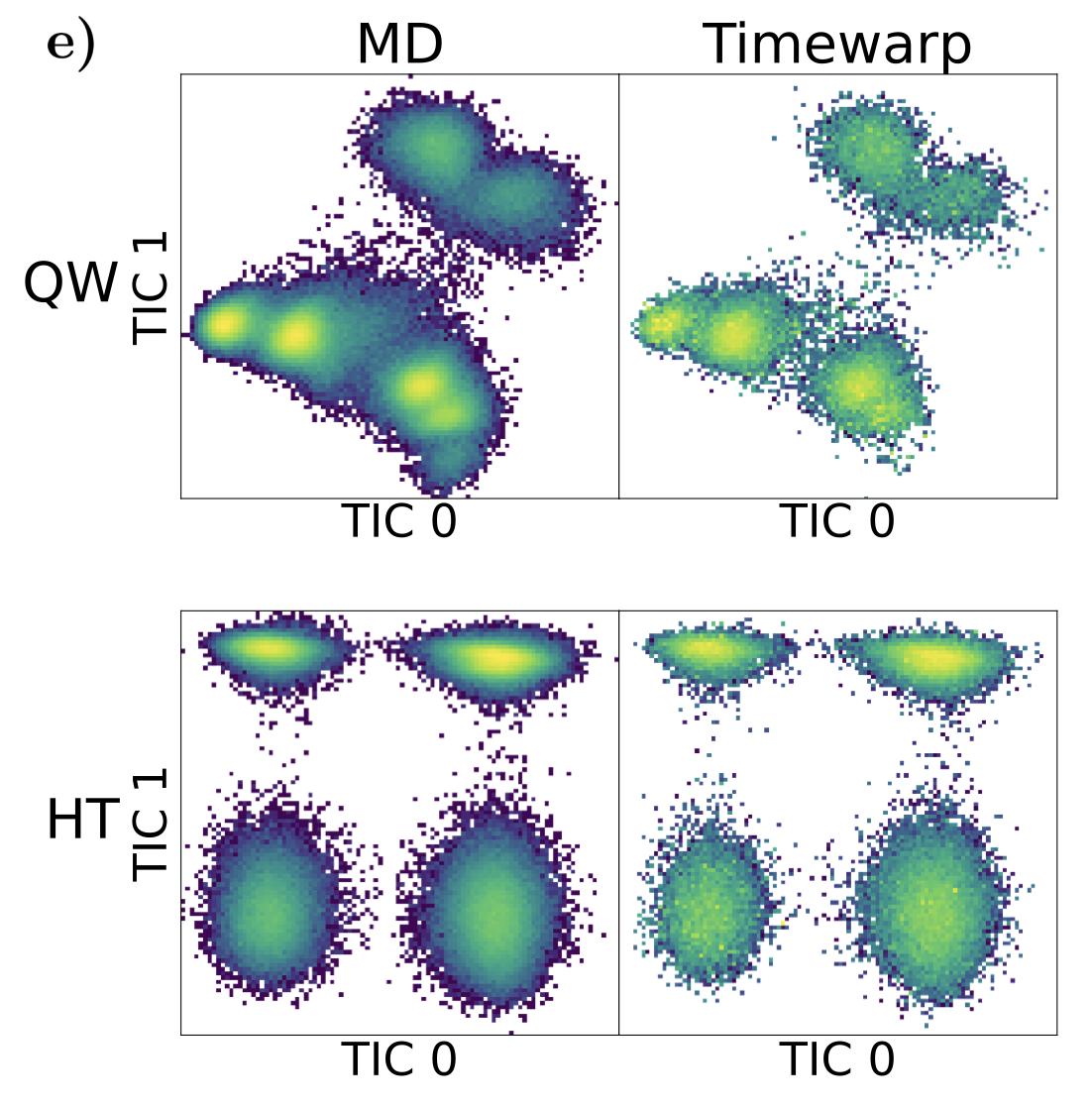
Timewarp: Transferable Acceleration of Molecular Dynamics by Learning Time-Coarsened Dynamics
Neural Information Processing Systems (neurips) spotlight presentation
Leon Klein†, Andrew Y. K. Foong†, Tor Erlend Fjelde†, Bruno Mlodozeniec†, Marc Brockschmidt, Sebastian Nowozin, Frank Noé, Ryota Tomioka
Timewarp accelerates molecular dynamics simulations by using machine learning to predict longer-time dynamics directly, enabling researchers to efficiently explore protein behavior occurring over biologically relevant timescales. Uniquely, its learned dynamics are transferable across different molecular systems, significantly reducing computational time and enabling rapid investigation of protein folding and binding processes relevant to drug discovery.
abstract
Molecular dynamics (md) simulation is a widely used technique to simulate molecular systems, most commonly at the all-atom resolution where the equations of motion are integrated with timesteps on the order of femtoseconds (1 fs = 10−15 s). md is often used to compute equilibrium properties, which requires sampling from an equilibrium distribution such as the Boltzmann distribution. However, many important processes, such as binding and folding, occur over timescales of milliseconds or beyond, and cannot be efficiently sampled with conventional md. Furthermore, new md simulations need to be performed from scratch for each molecular system studied. We present Timewarp, an enhanced sampling method which uses a normalising flow as a proposal distribution in a Markov chain Monte Carlo method targeting the Boltzmann distribution. The flow is trained offline on md trajectories and learns to make large steps in time, simulating the molecular dynamics of 105−106 fs. Crucially, Timewarp is transferable between molecular systems: once trained, we show that it generalises to unseen small peptides (2–4 amino acids), exploring their metastable states and providing wall-clock acceleration when sampling compared to standard md. Our method constitutes an important step towards developing general, transferable algorithms for accelerating md.
2022

Approximate Inference in Bayesian Neural Networks and Translation Equivariant Neural Processes
ph.d. thesis, University of Cambridge
Andrew Y. K. Foong
This thesis investigates two probabilistic frameworks for modelling uncertainty in machine learning, Bayesian neural networks and neural processes, and highlights both theoretical limits and architectural advances. It shows where popular inference methods fall short in capturing uncertainty, and introduces Convolutional Neural Processes, which leverage spatial symmetries to improve predictions when structure in the data allows.
abstract
It has been a longstanding goal in machine learning to develop flexible prediction methods that ‘know what they don’t know’—when faced with an out-of-distribution input, these models should signal their uncertainty rather than be confidently wrong. This thesis is concerned with two such probabilistic machine learning models: Bayesian neural networks and neural processes. Bayesian neural networks are a classical model that has been the subject of research since the 1990s. They rely on Bayesian inference to represent uncertainty in the weights of a neural network. On the other hand, neural processes are a recently introduced model that relies on meta-learning rather than Bayesian inference to obtain uncertainty estimates. This thesis provides contributions to both of these research areas. For Bayesian neural networks, we provide a theoretical and empirical study of the quality of common variational methods in approximating the Bayesian predictive distribution. We show that for single-hidden layer networks with relu activation functions, there are fundamental limitations concerning the representation of in-between uncertainty: increased uncertainty in between well separated regions of low uncertainty. We show that this theoretical limitation doesn’t apply for deeper networks. However, in practice, in-between uncertainty is a feature of the exact predictive distribution that is still often lost by approximate inference, even with deep networks. In the second part of this thesis, we focus on neural processes. In contrast to Bayesian neural networks, neural processes do not rely on approximate inference. Instead, they use neural networks to directly parameterise the map from a dataset to the posterior predictive stochastic process conditioned on that dataset. In this thesis we introduce the convolutional neural process, a new kind of neural process architecture which incorporates translation equivariance into its predictions. We show that when this symmetry is an appropriate assumption, convolutional neural processes outperform their standard multilayer perceptron-based and attentive counterparts on a variety of regression benchmarks.
2021
Collapsed Variational Bounds for Bayesian Neural Networks
Neural Information Processing Systems (neurips)
Marcin B. Tomczak, Siddharth Swaroop, Andrew Y. K. Foong, Richard E. Turner
This paper introduces tighter variational bounds for Bayesian neural networks by treating prior parameters as latent variables and collapsing the bound analytically. The result is improved performance of mean-field variational inference in deep models along with a more principled way to learn hierarchical priors.
abstract
Recent interest in learning large variational Bayesian Neural Networks (bnns) has been partly hampered by poor predictive performance caused by underfitting, and their performance is known to be very sensitive to the prior over weights. Current practice often fixes the prior parameters to standard values or tunes them using heuristics or cross-validation. In this paper, we treat prior parameters in a distributional way by extending the model and collapsing the variational bound with respect to their posteriors. This leads to novel and tighter Evidence Lower Bounds (elbos) for performing variational inference (vi) in (bnns). Our experiments show that the new bounds significantly improve the performance of Gaussian mean-field vi applied to (bnns) on a variety of data sets, demonstrating that mean-field vi works well even in deep models. We also find that the tighter (elbos) can be good optimization targets for learning the hyperparameters of hierarchical priors.
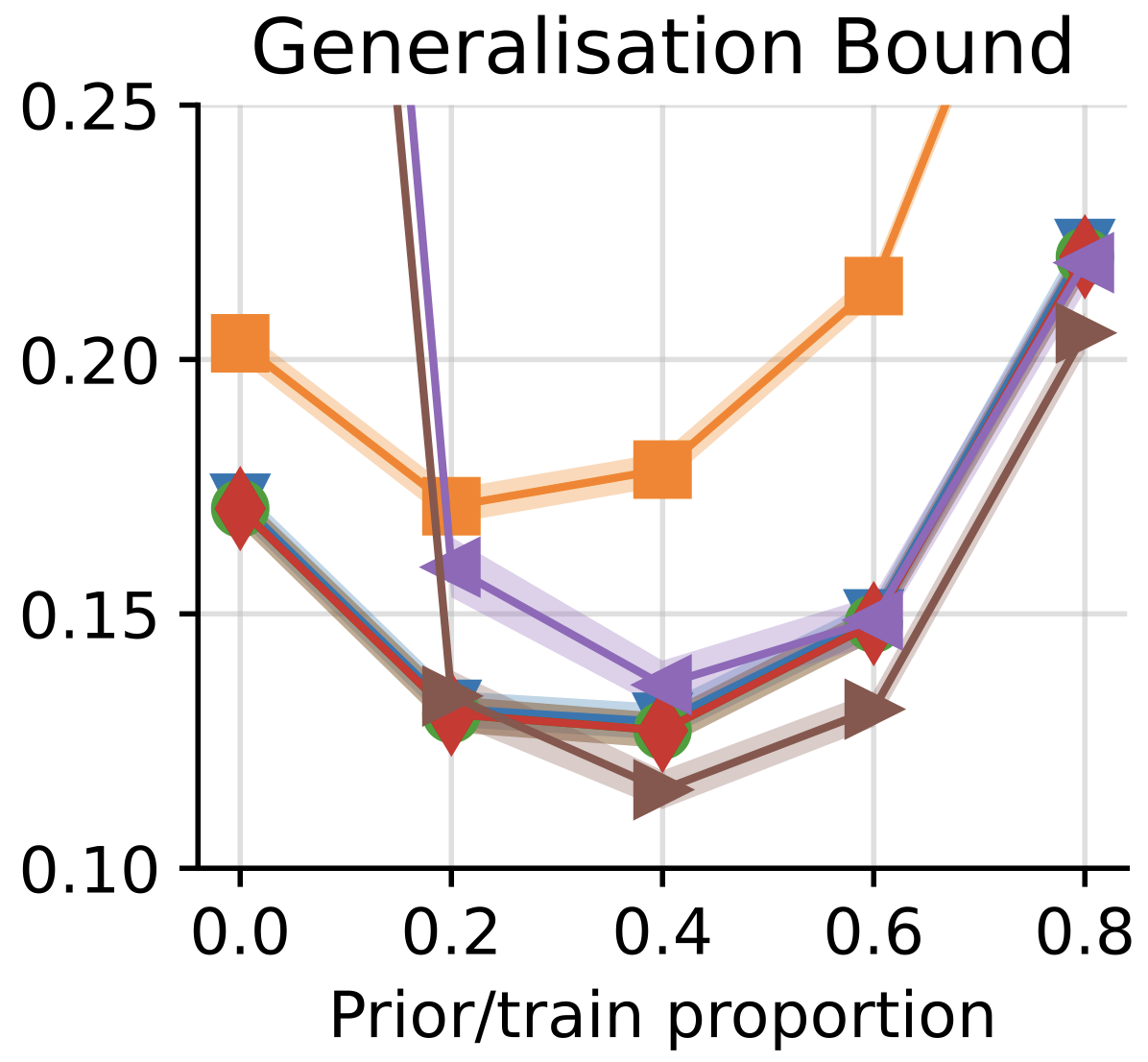
How Tight Can PAC-Bayes be in the Small Data Regime?
Neural Information Processing Systems (neurips)
Andrew Y. K. Foong†, Wessel P. Bruinsma†, David R. Burt, and Richard E. Turner
This paper investigates how tight pac-Bayes bounds (tools used to estimate generalization error) can be when applied to small datasets, where each data point matters greatly. It reveals unexpected theoretical limits on pac-Bayes performance, demonstrating that while pac-Bayes bounds outperform standard test-set methods by using all available data, they still fall short of optimal test-set bounds in highly controlled scenarios.
abstract
In this paper, we investigate the question: Given a small number of datapoints, for example n = 30, how tight can pac-Bayes and test set bounds be made? For such small datasets, test set bounds adversely affect generalisation performance by discarding data. In this setting, pac-Bayes bounds are especially attractive, due to their ability to use all the data to simultaneously learn a posterior and bound its generalisation risk. We focus on the case of i.i.d. data with a bounded loss and consider the generic pac-Bayes theorem of Germain et al. (2009) and Begin et al. (2016). While their theorem is known to recover many existing pac-Bayes bounds, it is unclear what the tightest bound derivable from their framework is. Surprisingly, we show that for a fixed learning algorithm and dataset, the tightest bound of this form coincides with the tightest bound of the more restrictive family of bounds considered in Catoni (2007). In contrast, in the more natural case of distributions over datasets, we give examples (both analytic and numerical) showing that the family of bounds in Catoni (2007) can be suboptimal. Within the proof framework of Germain et al. (2009) and Begin et al. (2016), we establish a lower bound on the best bound achievable in expectation, which recovers the Chernoff test set bound in the case when the posterior is equal to the prior. Finally, to illustrate how tight these bounds can potentially be, we study a synthetic one-dimensional classification task in which it is feasible to meta-learn both the prior and the form of the bound to obtain the tightest pac-Bayes and test set bounds possible. We find that in this simple, controlled scenario, pac-Bayes bounds are surprisingly competitive with comparable, commonly used Chernoff test set bounds. However, the sharpest test set bounds still lead to better guarantees on the generalisation error than the pac-Bayes bounds we consider.
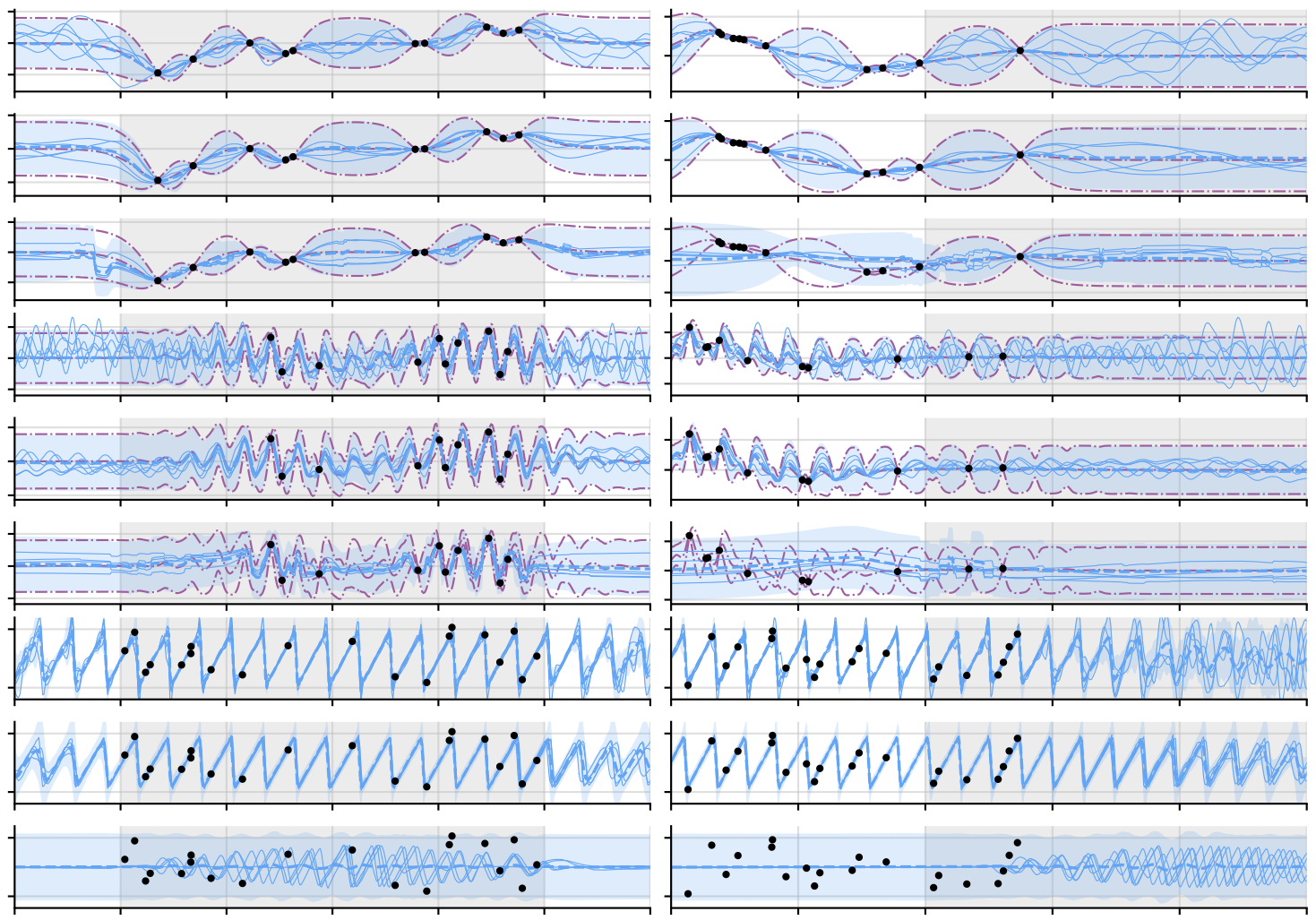
The Gaussian Neural Process
Advances in Approximate Bayesian Inference (aabi)
Wessel P. Bruinsma, James Requeima, Andrew Y. K. Foong, Jonathan Gordon, and Richard E. Turner
This paper introduces the Gaussian Neural Process, a new model that captures correlations in predictions and incorporates translation symmetry. By addressing key limitations of existing Neural Processes, the Gaussian Neural Process improves predictive accuracy, broadening their applicability in meta-learning and tasks requiring robust uncertainty estimation.
abstract
Neural Processes (nps; Garnelo et al., 2018a,b) are a rich class of models for meta-learning that map data sets directly to predictive stochastic processes. We provide a rigorous analysis of the standard maximum-likelihood objective used to train conditional nps. Moreover, we propose a new member to the Neural Process family called the Gaussian Neural Process (gnp), which models predictive correlations, incorporates translation equivariance, provides universal approximation guarantees, and demonstrates encouraging performance.
2020
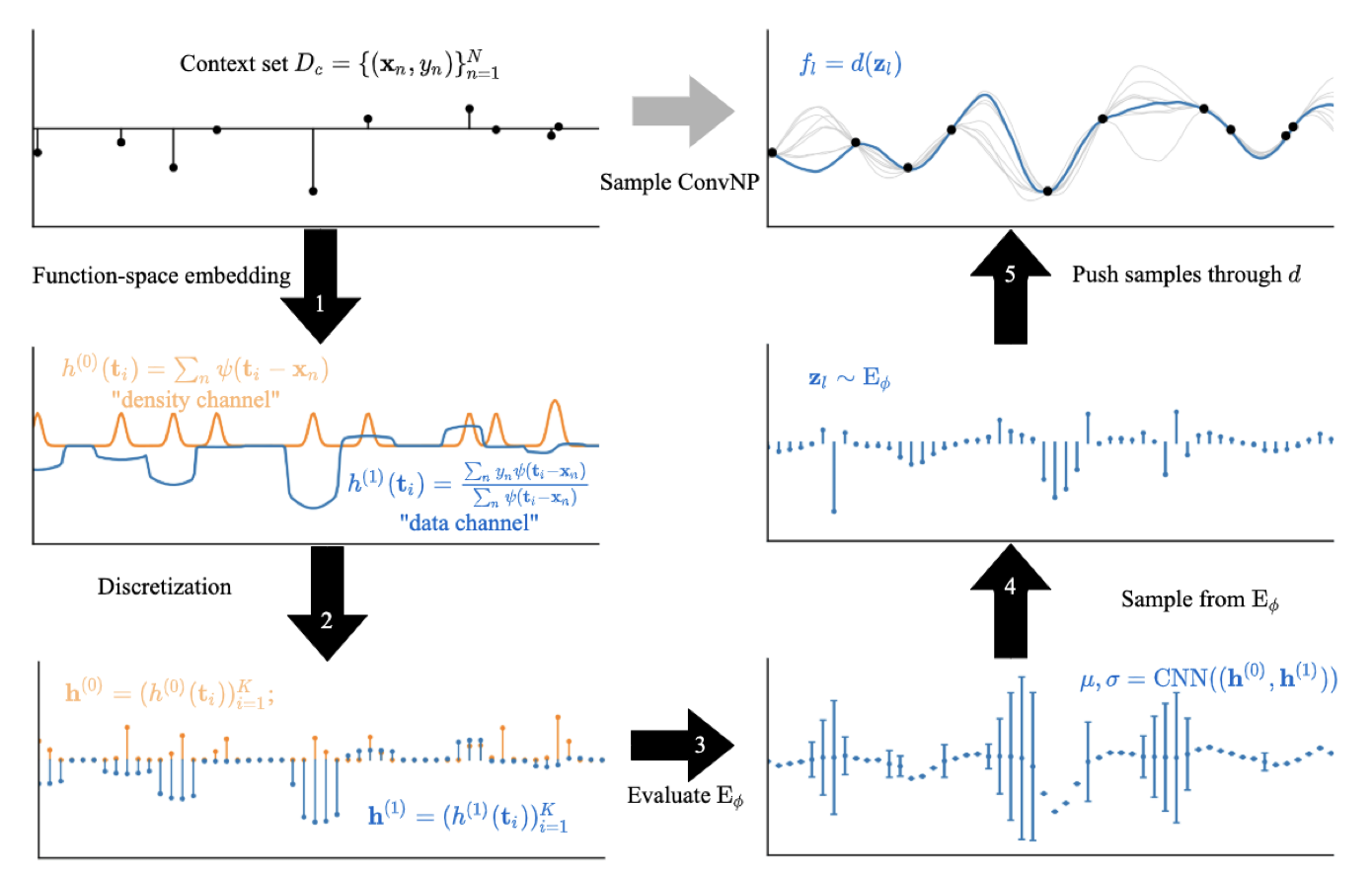
Meta-Learning Stationary Stochastic Process Prediction with Convolutional Neural Processes
Neural Information Processing Systems (neurips)
Andrew Y. K. Foong†, Wessel P. Bruinsma†, Jonathan Gordon†, Yann Dubois, James Requeima, and Richard E. Turner
This follow-up paper builds on Convcnps by enabling predictions that capture dependencies in structured data, improving coherence in tasks like image completion and spatio-temporal forecasting. Convnps also introduce a simpler and more effective training approach for latent variable models compared with previous latent neural process models.
abstract
Stationary stochastic processes (sps) are a key component of many probabilistic models, such as those for off-the-grid spatio-temporal data. They enable the statistical symmetry of underlying physical phenomena to be leveraged, thereby aiding generalization. Prediction in such models can be viewed as a translation equivariant map from observed data sets to predictive sps, emphasizing the intimate relationship between stationarity and equivariance. Building on this, we propose the Convolutional Neural Process (Convnp), which endows Neural Processes (nps) with translation equivariance and extends convolutional conditional nps to allow for dependencies in the predictive distribution. The latter enables Convnps to be deployed in settings which require coherent samples, such as Thompson sampling or conditional image completion. Moreover, we propose a new maximum-likelihood objective to replace the standard elbo objective in nps, which conceptually simplifies the framework and empirically improves performance. We demonstrate the strong performance and generalization capabilities of Convnps on 1d regression, image completion, and various tasks with real-world spatio-temporal data.
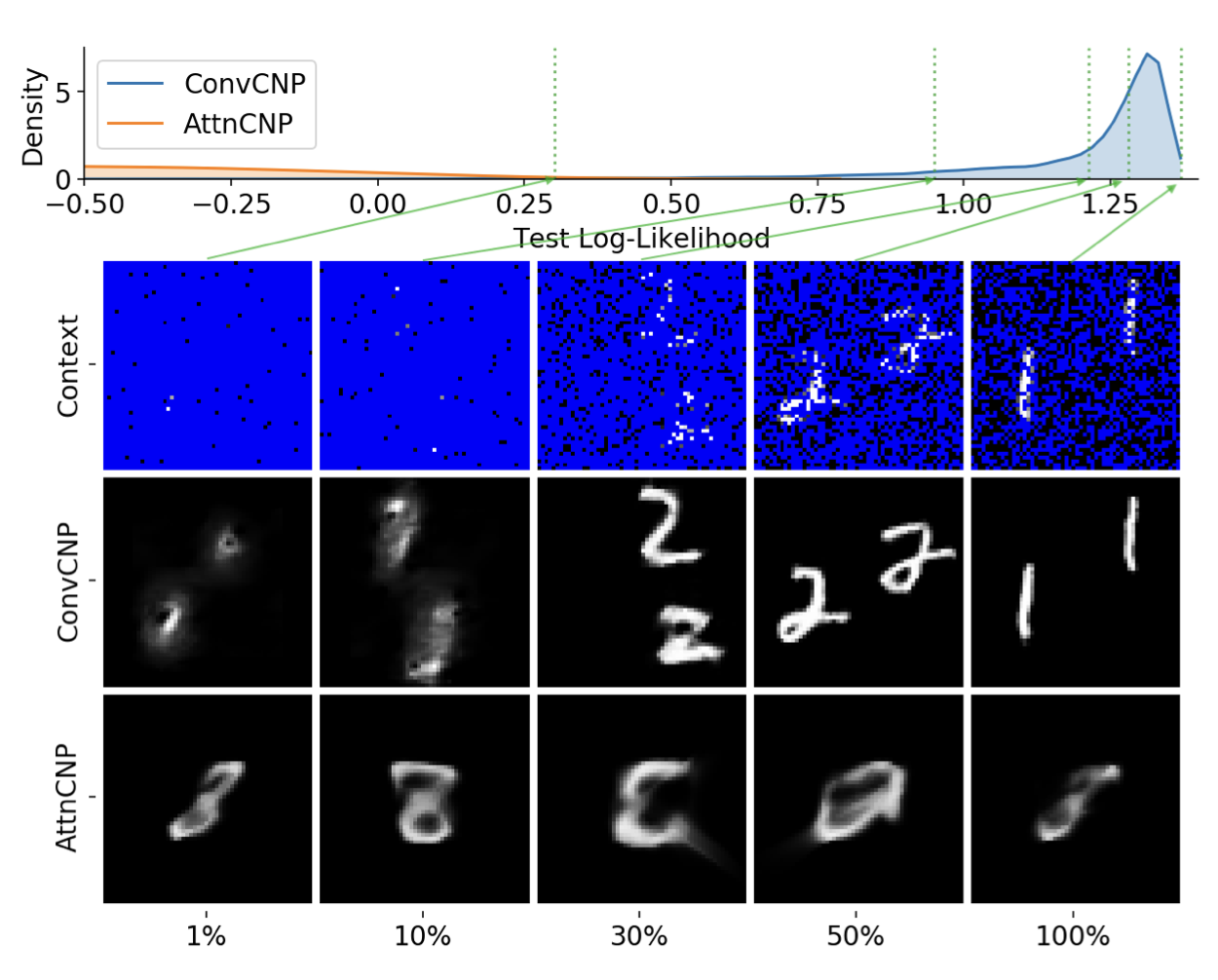
Convolutional Conditional Neural Processes
International Conference on Learning Representations (iclr)
Jonathan Gordon†, Wessel P. Bruinsma†, Andrew Y. K. Foong, James Requeima, Yann Dubois, and Richard E. Turner
This paper introduces the Convolutional Conditional Neural Process (Convcnp), a neural-network alternative to Gaussian processes, designed for reliable predictions when data is scarce or uncertainty matters. By incorporating translation symmetry, Convcnps accurately capture patterns in structured data, such as images or time series, and provides meaningful uncertainty estimates even on tasks it hasn’t encountered before.
abstract
We introduce the Convolutional Conditional Neural Process (Convcnp), a new member of the Neural Process family that models translation equivariance in the data. Translation equivariance is an important inductive bias for many learning problems including time series modeling, spatial data, and images. The model embeds data sets into an infinite-dimensional function space as opposed to a finite-dimensional vector space. To formalize this notion, we extend the theory of neural representations of sets to include functional representations, and demonstrate that any translation-equivariant embedding can be represented using a convolutional deep set. We evaluate Convcnps in several settings, demonstrating that they achieve state-of-the-art performance compared to existing nps. We demonstrate that building in translation equivariance enables zero-shot generalization to challenging, out-of-domain tasks.
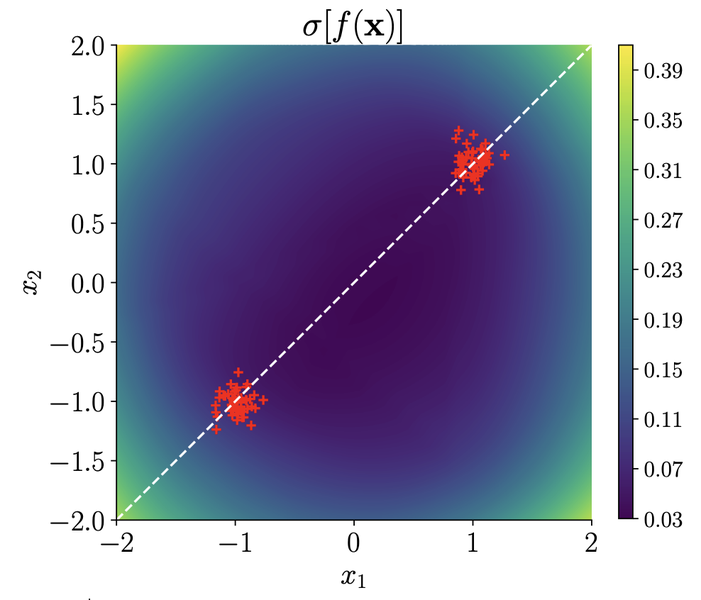
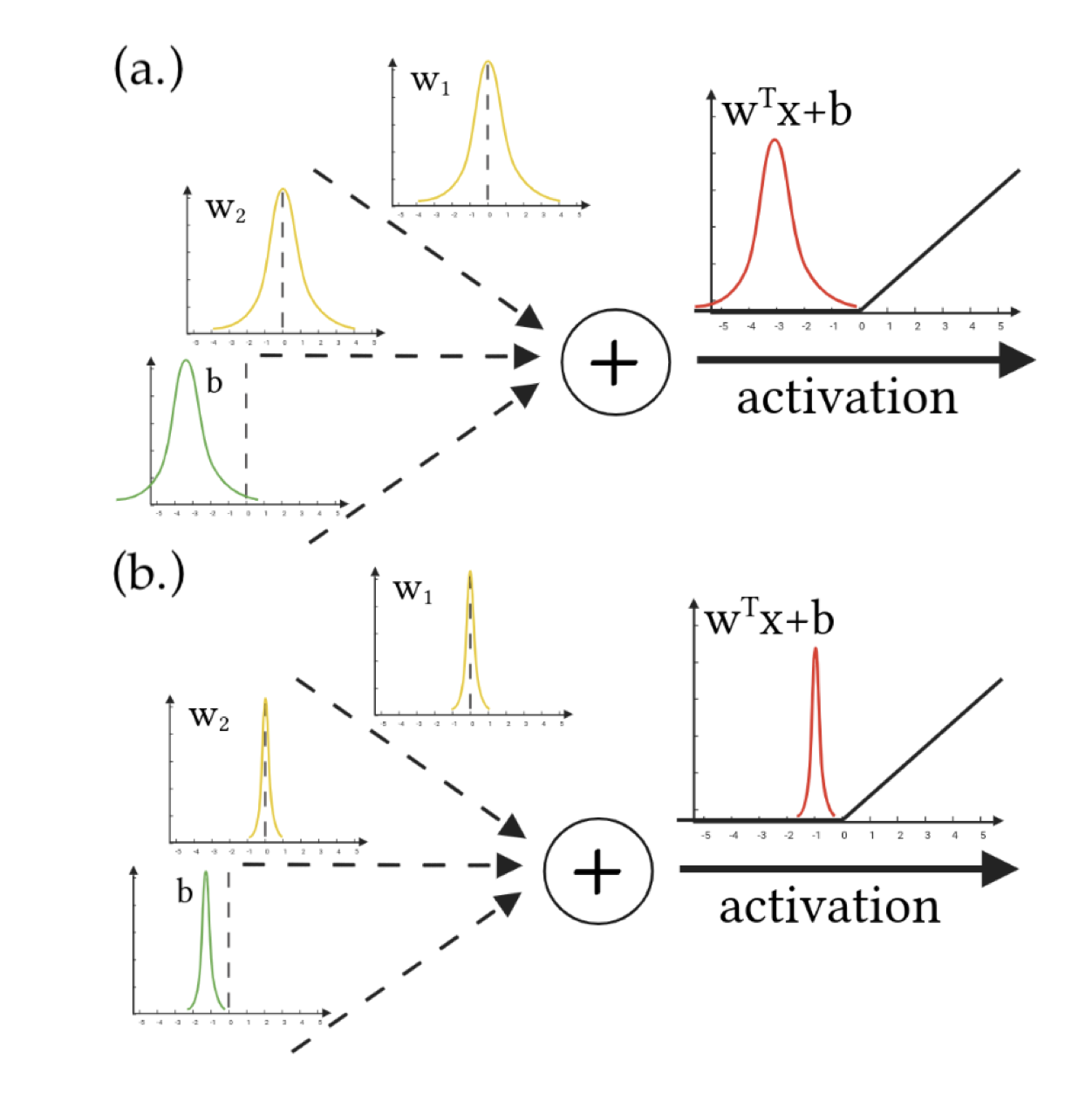
On the Expressiveness of Approximate Inference in Bayesian Neural Networks
Neural Information Processing Systems (neurips)
Andrew Y. K. Foong†, David R. Burt†, Yingzhen Li, Richard E. Turner
This paper explores critical limitations of commonly-used approximation methods in Bayesian neural networks (bnns), highlighting cases where these methods fail to represent uncertainty accurately. It reveals that although deeper networks theoretically overcome some limitations, problems persist in practice, emphasizing the need for caution when using approximate inference to obtain reliable uncertainty estimates from bnns.
abstract
While Bayesian neural networks (bnns) hold the promise of being flexible, well-calibrated statistical models, inference often requires approximations whose consequences are poorly understood. We study the quality of common variational methods in approximating the Bayesian predictive distribution. For single-hidden layer relu bnns, we prove a fundamental limitation in function-space of two of the most commonly used distributions defined in weight-space: mean-field Gaussian and Monte Carlo dropout. We find there are simple cases where neither method can have substantially increased uncertainty in between well-separated regions of low uncertainty. We provide strong empirical evidence that exact inference does not have this pathology, hence it is due to the approximation and not the model. In contrast, for deep networks, we prove a universality result showing that there exist approximate posteriors in the above classes which provide flexible uncertainty estimates. However, we find empirically that pathologies of a similar form as in the single-hidden layer case can persist when performing variational inference in deeper networks. Our results motivate careful consideration of the implications of approximate inference methods in bnns.
2019
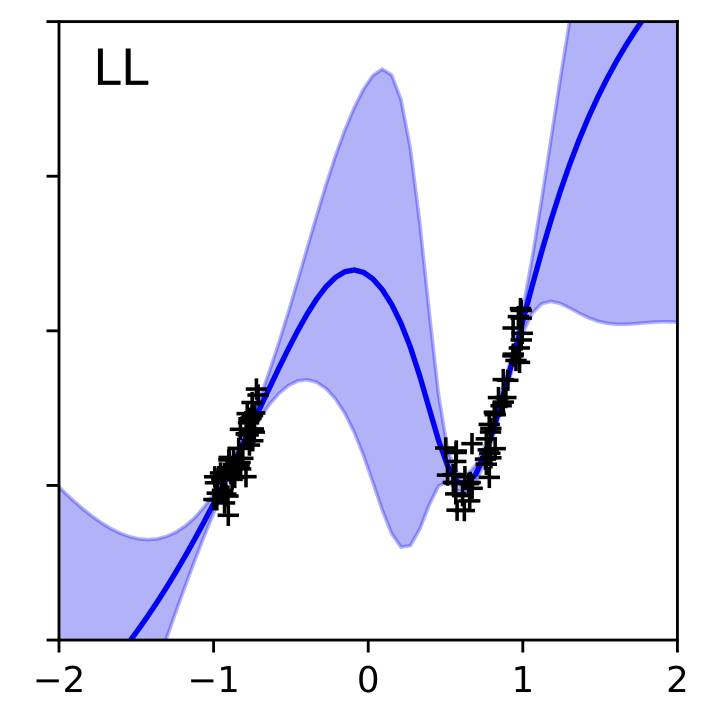
“In-Between” Uncertainty in Bayesian Neural Networks
icml Workshop on Uncertainty and Robustness in Deep Learning
Andrew Y. K. Foong, Yingzhen Li, José Miguel Hernández-Lobato, and Richard E. Turner
This paper identifies a critical flaw in how popular Bayesian neural network methods (like mean-field variational inference) estimate uncertainty, particularly when predicting outside known data regions. It shows that classical approaches, like the linearised Laplace approximation, handle such “in-between” uncertainty more reliably, improving trustworthiness in safety-critical applications.
abstract
We describe a limitation in the expressiveness of the predictive uncertainty estimate given by mean-field variational inference (mfvi), a popular approximate inference method for Bayesian neural networks. In particular, mfvi fails to give calibrated uncertainty estimates in between separated regions of observations. This can lead to catastrophically overconfident predictions when testing on out-of-distribution data. Avoiding such overconfidence is critical for active learning, Bayesian optimisation and out-of-distribution robustness. We instead find that a classical technique, the linearised Laplace approximation, can handle “in-between” uncertainty much better for small network architectures.
Talks
A collection of my publicly available presentations and slide decks.
2025

AI in the Clinic: What Could Go Wrong, and How We Can Catch It
mayo clinic quality & safety grand roundsThis talk explores case studies of past ai implementation failures in healthcare and how we can avoid them in the future. I provide general principles for how to think through a rational approach to the enormous opportunities, but also risks, that ai in healthcare poses. View the slides.
Scalable Emulation of Protein Equilibrium Ensembles with Generative Deep Learning
mayo clinic biochemistry & molecular biology seminar seriesThis talk provides an introduction to BioEmu, starting with AlphaFold and the deep learning revolution in protein structure, to the necessity of dynamics and conformational change prediction. I describe the training data, model architecture and capabilities of BioEmu. View the slides.
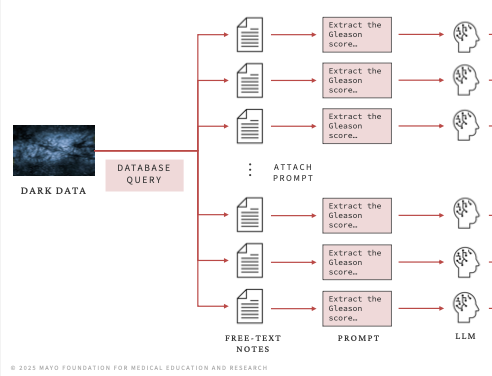
Reading Clinical Notes with AI: Building an Effective System
mayo clinic ai lunch & learn seriesEnormous volumes of clinical data are stored in free-text clinical notes that cannot be queried or statistically analyzed without painstaking human review. This dark data can now be accessed at scale using large language models. This talk, delivered to clinicians, explains best practices for building reliable workflows to extract this data. View the slides.
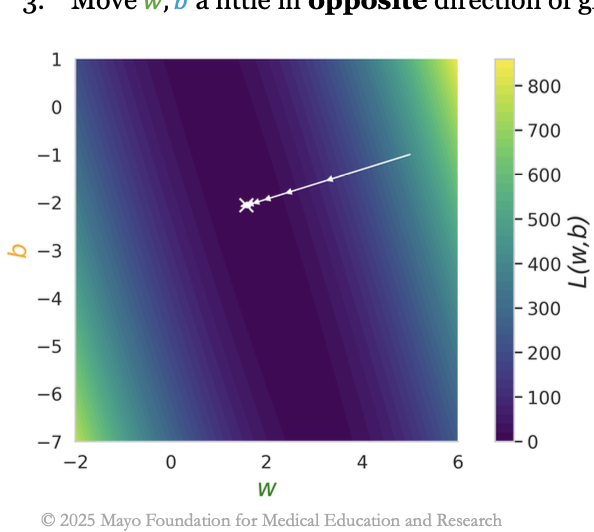
The Emergence of AI in Healthcare
mayo clinic ai selective courseThis lecture—the first in a selective course delivered to students at the Mayo Clinic—provides a concise introduction to deep learning, explaining gradient descent, and how large language models are trained and generate text. View the slides.
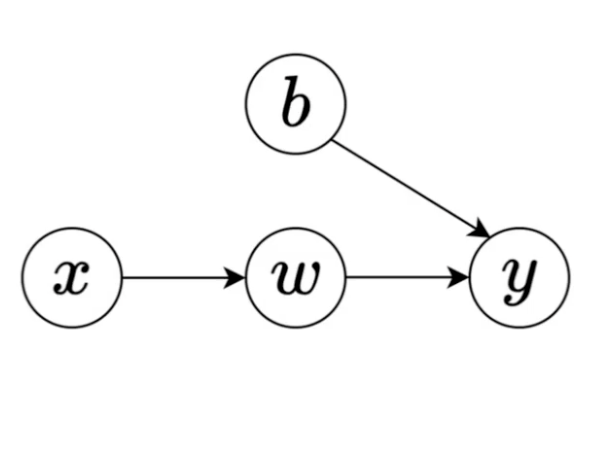
Understanding AI from Scratch
mayo clinic lecture series
I designed this six-part series to help clinicians at the Mayo Clinic with no prior ai experience understand deep learning from first principles.
lectures 1 & 2 cover deep learning from the ground up, from linear regression and gradient descent to neural networks, overfitting, and generalization.
lectures 3 & 4 explain what convolutional neural networks are and how they can be used to understand images.
lectures 5 & 6 explain how Chatgpt works, how it was made, and how prompting and retrieval-augmented generation (rag) can increase accuracy.
2023

Timewarp: Transferable Acceleration of Molecular Dynamics by Learning Time-Coarsened Dynamics
online reading group presentationCo-first author Leon Klein and I presented our neurips 2023 spotlight paper on using deep learning to accelerate molecular dynamics simulation at two online reading groups.
2021
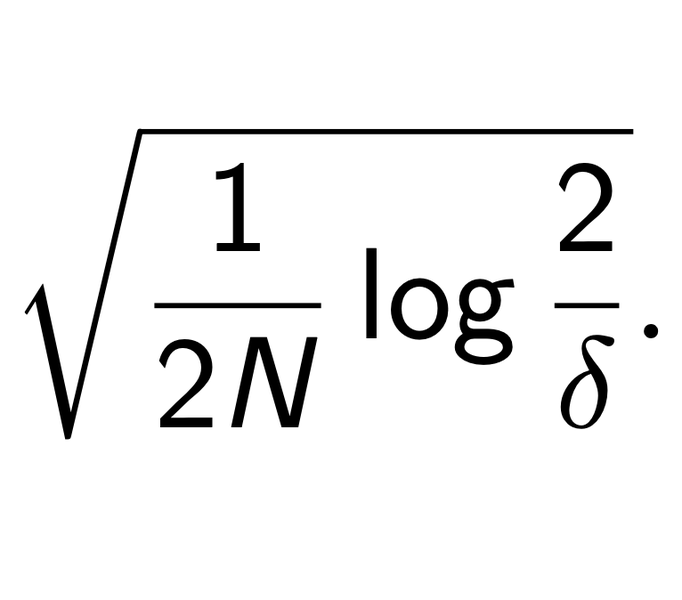
An Introduction to PAC-Bayes
cambridge machine learning reading groupI gave an introductory talk on the statistical learning framework and pac-Bayes with David Burt and Javier Antoran. View the slides.
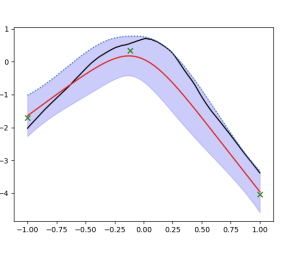
Understanding Approximate Inference in Bayesian Neural Networks
joint talk with oxford universityI gave a talk on my neurips 2020 paper on approximate inference in Bayesian neural networks, with an accompanying talk by Sebastian Farquhar of the University of Oxford. Our talks present different perspectives on the effectiveness of the mean-field approximation in these models. View the slides.
2020

On the Expressiveness of Approximate Inference in Bayesian Neural Networks
presentation at neurips conferenceA short video describing my paper on flaws in uncertainty estimation when using common approximate Bayesian neural network inference methods.

Meta-learning Stationary Stochastic Process Prediction with Convolutional Neural Processes
presentation at neurips conferenceA short video explaining my paper on neural processes, a deep learning alternative to Gaussian processes for regression problems with uncertainty.
Neural Processes
cambridge machine learning reading groupA reading group talk given with Sebastian Ober and Stratis Markou, introducing various neural processes and covering much of the material in this blog post. View the slides.

Recent Advances in Bayesian Deep Learning
cambridge machine learning reading groupA reading group talk given with Siddharth Swaroop, covering modern stochastic gradient Markov chain Monte Carlo (sgmcmc) and natural gradient variational inference methods for Bayesian deep learning. View the slides.
2019

“In-Between” Uncertainty in Bayesian Neural Networks
contributed talk, icml workshop on uncertainty in deep learningA contributed talk explaining my paper on the lack of “in-between” uncertainty when using the mean-field approximation in Bayesian neural networks. Watch the video (beginning at 28:30), or view the slides.

Implicit Variational Inference
cambridge machine learning reading groupI gave a talk with David Burt introducing implicit variational inference, a way to obtain very flexible approximate posterior distributions for Bayesian inference. View the slides.
Blog Posts
Occasional writings and tutorials on machine learning.MLP Weight Evolution Visualizer
This tool allows you to view the weights of a small three-layer mlp evolve as it trains on the mnist dataset. Created as an educational aid for an ai lecture course at the Mayo Clinic.
The Neural Process Family
Yann Dubois, Jonathan Gordon, Andrew Y. K. Foong
Deep learning shines when there’s lots of data, but fails in low-data settings where uncertainty matters, commonly encountered in medical time-series. Neural processes are a family of models that tackles this by meta-learning a distribution over predictors, blending stochastic processes with neural networks. This site walks through the ideas, maths, and code from scratch.
What Keeps a Bayesian Awake at Night?
Wessel P. Bruinsma, Andrew Y. K. Foong, Richard E. Turner
A two-part blog exploring the sunny arguments for Bayesian inference, and then, in part two, taking a critical perspective. Written by members of an avowedly Bayesian Cambridge research group, we look at where the theory breaks, the modelling compromises we make, and the computational hurdles that keep us up at night.
part 1: day | part 2: night
Curriculum Vitae
My academic cv is available as a pdf here.
Last updated January 2025.